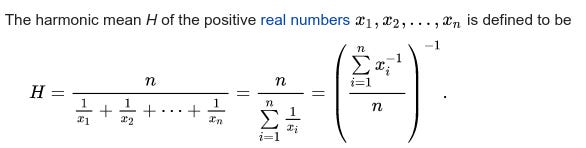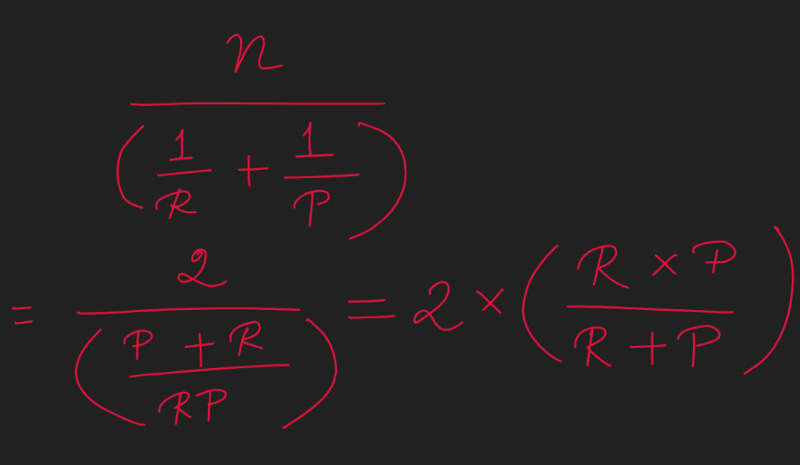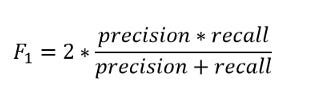Why F1 Score uses Harmonic Mean and not an Arithmetic Mean

Definition of Harmonic Mean

It is calculated by dividing the number of observations by the reciprocal of each number in the series. Thus, the harmonic mean is the reciprocal of the arithmetic mean of the reciprocals.

The harmonic mean helps to find multiplicative or divisor relationships between fractions without worrying about common denominators. Harmonic means are often used in averaging things like rates (e.g., the average travel speed given a duration of several trips).

Harmonic means are used in finance to average data like price multiples.

Harmonic means can also be used by market technicians to identify patterns such as Fibonacci sequences.

So for case of 2 variables, Recall (R) and Precision(P) — It becomes the below

And thats the formula of F1 Score

The F1 score is the harmonic mean of precision and recall, taking both metrics into account in the following equation:

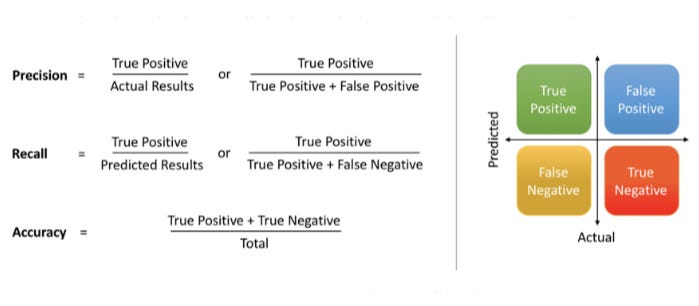
Now some basic definitions

So when Precision is 0.943 — This means if Models predict that a patient has heart disease, it is correct around 94% of the time.

Precision also gives us a measure of the relevant data points. It is important that we don’t start treating a patient who actually doesn’t have a heart ailment, but our model predicted as having it.

Recall = 0.76. Recall also gives a measure of how accurately our model is able to identify the relevant data. We refer to it as Sensitivity or True Positive Rate. What if a patient has heart disease, but there is no treatment given to him/her because our model predicted so? That is a situation we would like to avoid!

So Recall accounts for False-Negative. And in preliminary disease screening — ideally, we don't want to have any False-Negative. This means someone who is actually Cancer-Positive but Model tells he is Cancer-negative is absolutely dangerous.

For example, for a Cancer Classification dataset (whether a patient is Cancer-Positive or Cancer-Negative) , we can consider that achieving a high recall is more important than getting a high precision — we would like to detect as many heart patients as possible. For some other models, like classifying whether a bank customer is a loan defaulter or not, it is desirable to have a high precision since the bank wouldn’t want to lose customers who were denied a loan based on the model’s prediction that they would be defaulters.

Ideally, you want both to be 1 for your model. That doesn’t happen in your real world datasets. In reality it is a zero-sum game. If you try to improve Precision, the Recall falls and vice-versa.

So, in preliminary disease screening of patients for follow-up examinations, we would probably want a recall near 1.0 — we want to find all patients who actually have the disease — and we can accept a low precision — we accidentally find some patients have the disease who actually don’t have it — if the cost of the follow-up examination isn’t high. However, in cases where we want to find an optimal blend of precision and recall, we can combine the two metrics using the F1 score.

Simply, We use the harmonic mean instead of a simple average because it punishes extreme values.

It is never higher than the geometrical mean. It also tends towards the least number, minimizing the impact of the large outliers and maximizing the impact of small ones. The F1-measure, therefore, tends to privilege balanced systems.

Consider a trivial method (e.g. always returning class A). There are infinite data elements of class B, and a single element of class A:

Precision: 0.0Recall:    1.0

When taking the arithmetic mean, it would have 50% correct. Despite being the worst possible outcome! With the harmonic mean, the F1-measure is 0.

Arithmetic mean: 0.5Harmonic mean:   0.0

In other words, to have a high F1, you need to both have a high precision and recall.

Take another example

Model with a Precision of 0.8 and Recall of 0.9.

So the AM = (0.8+0.9)/2=0.850

GM = sqrt(0.8 * 0.9)=0.849

HM = 2*(0.8*0.9)/(0.8+0.9)= 0.847

As we can see compared to AM and GM, HM penalizes model the most even when one of the metric out of Precision and Recall is low. Hence to have a high F1, you need to both have a high precision and recall.

So If we want to create a classification model with the optimal balance of recall and precision, then we try to maximize the F1 score.